Permutation / Combination - ACT Math
Card 0 of 19
In permutation notation, what does 8P4 represent?
In permutation notation, what does 8P4 represent?
The expression 8P4 represents the number of permutations of 8 objects arranged 4 at a time. Thus, 8 x 7 x 6 x 5 = 1680
The expression 8P4 represents the number of permutations of 8 objects arranged 4 at a time. Thus, 8 x 7 x 6 x 5 = 1680
Compare your answer with the correct one above
How many different ways can five books be lined up on a shelf?
How many different ways can five books be lined up on a shelf?
Order matters, so we use permutations: (5)(4)(3)(2)(1) = 120
There are five possibilities for the first book, four possibilities for the second book, three for the third, and two for the fourth, and one possibility for the last book.
Order matters, so we use permutations: (5)(4)(3)(2)(1) = 120
There are five possibilities for the first book, four possibilities for the second book, three for the third, and two for the fourth, and one possibility for the last book.
Compare your answer with the correct one above
How many different ways can cheese slices be stacked in piles containing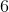 
unique types if you are presented with a selection of 
different cheeses? (Presume that the order of the cheese slices does matter.)
How many different ways can cheese slices be stacked in piles containing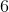
Since the order matters, you are dealing with a permutation in this question. A permutation like this could be done with the equation:
For our values, this would be:
However, it is easiest just to think of this like it has 
slots. Into the first, you have 
choices, into the second 
, and so forth. This generates for you
more easily.
This is 
. That is a lot of cheese arrangements!
Since the order matters, you are dealing with a permutation in this question. A permutation like this could be done with the equation:
For our values, this would be:
However, it is easiest just to think of this like it has
more easily.
This is
Compare your answer with the correct one above
Susie wants to make a sandwich for lunch. She has two types of breads, three types of meats, and two types of cheeses to choose from. How many different sandwiches can she make if she chooses only one of each ingredient?
Susie wants to make a sandwich for lunch. She has two types of breads, three types of meats, and two types of cheeses to choose from. How many different sandwiches can she make if she chooses only one of each ingredient?
Each item (bread, meat, and cheese) is chosen independently from the others, so the answer can be found in a tree diagram: Bread x Meat x Cheese or 2 x 3 x 2 or 12.
Each item (bread, meat, and cheese) is chosen independently from the others, so the answer can be found in a tree diagram: Bread x Meat x Cheese or 2 x 3 x 2 or 12.
Compare your answer with the correct one above
Ashley is modeling a new mix-and-match clothing line. Her stylist has selected 5 tops, 3 skirts, and 4 jackets for her photo shoot. Assuming that an outfit consists of one top, one skirt, and one jacket, how many outfits can Ashley create for the photo shoot?
Ashley is modeling a new mix-and-match clothing line. Her stylist has selected 5 tops, 3 skirts, and 4 jackets for her photo shoot. Assuming that an outfit consists of one top, one skirt, and one jacket, how many outfits can Ashley create for the photo shoot?
In order to calculate the total possible number of combinations, we must multiply the number of possibilities for each piece by one another.
In order to calculate the total possible number of combinations, we must multiply the number of possibilities for each piece by one another.
Compare your answer with the correct one above
How many different 5 letter computer passwords are possible, assuming that letters cannot be repeated?
How many different 5 letter computer passwords are possible, assuming that letters cannot be repeated?
26P5 = 26 x 25 x 24 x 23 x 22 = 7,893,600
26P5 = 26 x 25 x 24 x 23 x 22 = 7,893,600
Compare your answer with the correct one above
At a party with 9 guests, every guest shakes every other guest’s hand exactly once. How many handshakes are exchanged during the party?
When two people shake hands with each other, that counts as one handshake.
At a party with 9 guests, every guest shakes every other guest’s hand exactly once. How many handshakes are exchanged during the party?
When two people shake hands with each other, that counts as one handshake.
Each person shakes 8 people’s hands, so at first guess that’s 9x8=72 handshakes. However, this double counts the number of handshakes since we count the handshake between person A and B once when we count A’s 8 handshakes and a second time when we count B’s 8 handshakes. Therefore, we divide our estimate by 2 and get 36.
Each person shakes 8 people’s hands, so at first guess that’s 9x8=72 handshakes. However, this double counts the number of handshakes since we count the handshake between person A and B once when we count A’s 8 handshakes and a second time when we count B’s 8 handshakes. Therefore, we divide our estimate by 2 and get 36.
Compare your answer with the correct one above
A candy shop sells Valentine's Day gift baskets that consist of chocolates, a basket, and a card. If there are five different types of chocolate, three types of baskets, and ten options for cards, how many different gift basket combinations are there?
A candy shop sells Valentine's Day gift baskets that consist of chocolates, a basket, and a card. If there are five different types of chocolate, three types of baskets, and ten options for cards, how many different gift basket combinations are there?
The correct answer is 150. Since there are five types of chocolate, three types of baskets, and ten card choices, the correct answer can be found by multiplying 3 x 5 x 10, which is 150. If you got 15 or 1500, you may have made a multiplication error. If you got 18, you may have added instead of multiplying.
The correct answer is 150. Since there are five types of chocolate, three types of baskets, and ten card choices, the correct answer can be found by multiplying 3 x 5 x 10, which is 150. If you got 15 or 1500, you may have made a multiplication error. If you got 18, you may have added instead of multiplying.
Compare your answer with the correct one above
A student is taking a test consisting of six questions. It is a multiple choice test and each question has four answers labelled A, B, C, and D. How many ways can the student answer all six questions if he does not choose the same answer for any two consecutive questions?
A student is taking a test consisting of six questions. It is a multiple choice test and each question has four answers labelled A, B, C, and D. How many ways can the student answer all six questions if he does not choose the same answer for any two consecutive questions?
the student has four choices for the first question, but only three choices for each of the remaining questions since he does not choose answers with the same letter twice in a row. From the multiplicative counting principle, there are 4 × 3 × 3 × 3 × 3 x 3 = 972 ways Steve can answer the six questions.
the student has four choices for the first question, but only three choices for each of the remaining questions since he does not choose answers with the same letter twice in a row. From the multiplicative counting principle, there are 4 × 3 × 3 × 3 × 3 x 3 = 972 ways Steve can answer the six questions.
Compare your answer with the correct one above
A locker combination consists of three different numbers from the set of 30 different numbers on the face of the lock. Imagine that you have forgotten the combination. How many times do you have to try to find the right combination?
A locker combination consists of three different numbers from the set of 30 different numbers on the face of the lock. Imagine that you have forgotten the combination. How many times do you have to try to find the right combination?
It is said that the three numbers are different. So the number of lock combinations is 30_P_3 = 24 360.
It is said that the three numbers are different. So the number of lock combinations is 30_P_3 = 24 360.
Compare your answer with the correct one above
The game of euchre uses the 9s, 10s, jacks, queens, kings, and aces from a standard deck of 52 cards. How many 5-card euchre hands have at least 2 black cards?
The game of euchre uses the 9s, 10s, jacks, queens, kings, and aces from a standard deck of 52 cards. How many 5-card euchre hands have at least 2 black cards?
The hand could have 2, 3, 4, or 5 black cards. There are 12 black cards and 12 red cards, so the numbers of combinations for the four cases are as follows.
2 black cards: C(12, 2) × C(12, 3) = 14 520
3 black cards: C(12, 3) × C(12, 2) = 14 520
4 black cards: C(12, 4) × C(12, 1) = 5940
5 black cards: C(12, 5) × C(12, 0) = 792
The total number of euchre hands that have at least two black cards is the total of these four cases, 35 772.
The hand could have 2, 3, 4, or 5 black cards. There are 12 black cards and 12 red cards, so the numbers of combinations for the four cases are as follows.
2 black cards: C(12, 2) × C(12, 3) = 14 520
3 black cards: C(12, 3) × C(12, 2) = 14 520
4 black cards: C(12, 4) × C(12, 1) = 5940
5 black cards: C(12, 5) × C(12, 0) = 792
The total number of euchre hands that have at least two black cards is the total of these four cases, 35 772.
Compare your answer with the correct one above
You work as a health inspector and must visit each of the 15 restaurants in town once each week. In how many different orders can you make these inspections?
You work as a health inspector and must visit each of the 15 restaurants in town once each week. In how many different orders can you make these inspections?
15_P_15 = 15!
= 1.307 674 368 × 1012
15_P_15 = 15!
= 1.307 674 368 × 1012
Compare your answer with the correct one above
Sally is putting on jewelry and has decided to wear one necklace, one pair of earrings, and one ring. Her jewelry collection is listed below. How many different combinations of jewelry can she wear?
Necklace Earrings Ring short studs gold long hoops silver dangling
Sally is putting on jewelry and has decided to wear one necklace, one pair of earrings, and one ring. Her jewelry collection is listed below. How many different combinations of jewelry can she wear?
| Necklace | Earrings | Ring |
|---|---|---|
| short | studs | gold |
| long | hoops | silver |
| dangling |
To find the number of different combinations, we must use the fundamental counting principal to multiply the number of options in each category together:
(2)(3)(2) = 12
To find the number of different combinations, we must use the fundamental counting principal to multiply the number of options in each category together:
(2)(3)(2) = 12
Compare your answer with the correct one above
In how many ways can the seven members of a students’ council pose in a line for a yearbook photograph if the chair and vice-chair must be side by side?
In how many ways can the seven members of a students’ council pose in a line for a yearbook photograph if the chair and vice-chair must be side by side?
First find the number of arrangements in which the chair and vice-chair are together. Consider the chair and vice-chair as a unit. This pair as one unit can be arranged with the remaining five members in 
ways. For each of these ways, the chair could be either on the left or the right of the vice-chair.
Therefore, there is a total of 2 * 720 = 1440 ways in which the chair and vice-chair are together.
First find the number of arrangements in which the chair and vice-chair are together. Consider the chair and vice-chair as a unit. This pair as one unit can be arranged with the remaining five members in
Therefore, there is a total of 2 * 720 = 1440 ways in which the chair and vice-chair are together.
Compare your answer with the correct one above
A university can send 3 track athletes and 2 field athletes to an upcoming sports event. The university has 14 track athletes and 10 field athletes who qualify. How many different teams can be chosen to attend the sports event?
A university can send 3 track athletes and 2 field athletes to an upcoming sports event. The university has 14 track athletes and 10 field athletes who qualify. How many different teams can be chosen to attend the sports event?
The number of different teams that could be chosen is C(14, 3) × C(10, 2) = 16,380.
The number of different teams that could be chosen is C(14, 3) × C(10, 2) = 16,380.
Compare your answer with the correct one above
The menu above is from Lena’s Italian Kitchen. If you are going there for dinner, how many different combinations of a meal and a salad are there?
The menu above is from Lena’s Italian Kitchen. If you are going there for dinner, how many different combinations of a meal and a salad are there?
Combinations = # first option * # second option
= # meals * # salads
= 5 * 4 = 20
Combinations = # first option * # second option
= # meals * # salads
= 5 * 4 = 20
Compare your answer with the correct one above
A license plate consists of three letters followed by three numbers (excluding 0). How many license plates can be made if no letters or numbers are repeated?
A license plate consists of three letters followed by three numbers (excluding 0). How many license plates can be made if no letters or numbers are repeated?
There are 26 letters in the alphabet and 9 digits when you exclude 0. Each selection can go with any other selection, so each number is multiplied together. After the first letter is picked, the sample size (what you can pick from) is reduced by one because there is no repetition. So the answer 26 x 25 x 24 x 9 x 8 x 7 is correct. If repetition were allowed answer 26 x 26 x 26 x 9 x 9 x 9 would be correct.
There are 26 letters in the alphabet and 9 digits when you exclude 0. Each selection can go with any other selection, so each number is multiplied together. After the first letter is picked, the sample size (what you can pick from) is reduced by one because there is no repetition. So the answer 26 x 25 x 24 x 9 x 8 x 7 is correct. If repetition were allowed answer 26 x 26 x 26 x 9 x 9 x 9 would be correct.
Compare your answer with the correct one above
How many ways can 10 people win a race if ribbons are given for first, second, and third places?
How many ways can 10 people win a race if ribbons are given for first, second, and third places?
Independent events are multiplied. Once the first place is chosen, the sample space (what you can pick from) is reduced by one since there is no repetition (you can’t win first and second places at the same time). Thus, 10 x 9 x 8 = 720
Independent events are multiplied. Once the first place is chosen, the sample space (what you can pick from) is reduced by one since there is no repetition (you can’t win first and second places at the same time). Thus, 10 x 9 x 8 = 720
Compare your answer with the correct one above
Sam is getting dressed in the morning and has 6 pairs of pants, 4 shirts, and 5 pairs of socks to choose from. How many distinct combinations consisting of 1 pair of pants, 1 shirt and 1 pair of socks can Sam make?
Sam is getting dressed in the morning and has 6 pairs of pants, 4 shirts, and 5 pairs of socks to choose from. How many distinct combinations consisting of 1 pair of pants, 1 shirt and 1 pair of socks can Sam make?
In order to find the answer, multiply the quantities together:
This is because for each pair of pants, there are 4 options for shirts and 5 options for socks.
In order to find the answer, multiply the quantities together:
This is because for each pair of pants, there are 4 options for shirts and 5 options for socks.
Compare your answer with the correct one above