How to find the solution to a quadratic equation a1 - ACT Math
Card 0 of 20
Solve for x: 2(x + 1)2 – 5 = 27
Solve for x: 2(x + 1)2 – 5 = 27
Quadratic equations generally have two answers. We add 5 to both sides and then divide by 2 to get the quadratic expression on one side of the equation: (x + 1)2 = 16. By taking the square root of both sides we get x + 1 = –4 or x + 1 = 4. Then we subtract 1 from both sides to get x = –5 or x = 3.
Quadratic equations generally have two answers. We add 5 to both sides and then divide by 2 to get the quadratic expression on one side of the equation: (x + 1)2 = 16. By taking the square root of both sides we get x + 1 = –4 or x + 1 = 4. Then we subtract 1 from both sides to get x = –5 or x = 3.
Compare your answer with the correct one above
Solve 3x2 + 10x = –3
Solve 3x2 + 10x = –3
Generally, quadratic equations have two answers.
First, the equations must be put in standard form: 3x2 + 10x + 3 = 0
Second, try to factor the quadratic; however, if that is not possible use the quadratic formula.
Third, check the answer by plugging the answers back into the original equation.
Generally, quadratic equations have two answers.
First, the equations must be put in standard form: 3x2 + 10x + 3 = 0
Second, try to factor the quadratic; however, if that is not possible use the quadratic formula.
Third, check the answer by plugging the answers back into the original equation.
Compare your answer with the correct one above
Solve: 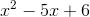
Solve:
To solve, we must set it equal to zero. The above expression is of the form  , so we can use the quadratic formula:
, so we can use the quadratic formula:

to solve for the roots which are  and
and 
We can check by plugging the roots into the expression and making sure that it equals zero.
To solve, we must set it equal to zero. The above expression is of the form 
to solve for the roots which are 
We can check by plugging the roots into the expression and making sure that it equals zero.
Compare your answer with the correct one above
What is the sum of the two solutions of the equation x2 + 5x – 24 = 0?
What is the sum of the two solutions of the equation x2 + 5x – 24 = 0?
First you must find the solutions to the equation. This can be done either by using the quadratic formula or by simply finding two numbers whose sum is 5 and whose product is -24 and factoring the equation into (x + 8)(x – 3) = 0. The solutions to the equation are therefore -8 and 3, giving a sum of -5.
First you must find the solutions to the equation. This can be done either by using the quadratic formula or by simply finding two numbers whose sum is 5 and whose product is -24 and factoring the equation into (x + 8)(x – 3) = 0. The solutions to the equation are therefore -8 and 3, giving a sum of -5.
Compare your answer with the correct one above
Solve for x: x2 + 4x = 5
Solve for x: x2 + 4x = 5
Solve by factoring. First get everything into the form Ax2 + Bx + C = 0:
x2 + 4x - 5 = 0
Then factor: (x + 5) (x - 1) = 0
Solve each multiple separately for 0:
X + 5 = 0; x = -5
x - 1 = 0; x = 1
Therefore, x is either -5 or 1
Solve by factoring. First get everything into the form Ax2 + Bx + C = 0:
x2 + 4x - 5 = 0
Then factor: (x + 5) (x - 1) = 0
Solve each multiple separately for 0:
X + 5 = 0; x = -5
x - 1 = 0; x = 1
Therefore, x is either -5 or 1
Compare your answer with the correct one above
If (x + a)(x + b) = x2 – 9x + 18, what are the values for a and b?
If (x + a)(x + b) = x2 – 9x + 18, what are the values for a and b?
a = _–_3, b = _–_6. The sum of a and b have to be equal to _–_9, and they have to multiply together to get +18. If a = _–_3 and b = _–6, (–3) + (–6) = (–9) and (–3)(–_6) = 18.
a = _–_3, b = _–_6. The sum of a and b have to be equal to _–_9, and they have to multiply together to get +18. If a = _–_3 and b = _–6, (–3) + (–6) = (–9) and (–3)(–_6) = 18.
Compare your answer with the correct one above
When asked how many home runs he hit in a season, Pablo Sanchez responded with, "If you square the number of home runs and subtract 50 times the number of home runs, it is equivalent to 50." How many home runs has Pablo hit?
When asked how many home runs he hit in a season, Pablo Sanchez responded with, "If you square the number of home runs and subtract 50 times the number of home runs, it is equivalent to 50." How many home runs has Pablo hit?
We can generate an equation for the number of home runs he has hit, x : x2 - 50x = 50. Reordering this, we get : x2 - 50x - 50 = 0. Using the quadratic equation: x = (-b± √(b2-4ac)) / (2a). In this case, a = 1, b = -50, c = -50. Plugging in these values, we obtain the simplified equation, x = (50±51.96)/2. Therefore, x = 50.98, -0.98. Because it doesn't make sense to have a negative number of home runs, x = 50.98, which rounds up to 51 home runs.
We can generate an equation for the number of home runs he has hit, x : x2 - 50x = 50. Reordering this, we get : x2 - 50x - 50 = 0. Using the quadratic equation: x = (-b± √(b2-4ac)) / (2a). In this case, a = 1, b = -50, c = -50. Plugging in these values, we obtain the simplified equation, x = (50±51.96)/2. Therefore, x = 50.98, -0.98. Because it doesn't make sense to have a negative number of home runs, x = 50.98, which rounds up to 51 home runs.
Compare your answer with the correct one above
Let  , and let
, and let  . What is the sum of the possible values of
. What is the sum of the possible values of  such that
such that  .
.
Let 



We are told that f(x) = x2 - 4x + 2, and g(x) = 6 - x. Let's find expressions for f(k) and g(k).
f(k) = k2 – 4k + 2
g(k) = 6 – k
Now, we can set these expressions equal.
f(k) = g(k)
k2 – 4k +2 = 6 – k
Add k to both sides.
k2 – 3k + 2 = 6
Then subtract 6 from both sides.
k2 – 3k – 4 = 0
Factor the quadratic equation. We must think of two numbers that multiply to give us -4 and that add to give us -3. These two numbers are –4 and 1.
(k – 4)(k + 1) = 0
Now we set each factor equal to 0 and solve for k.
k – 4 = 0
k = 4
k + 1 = 0
k = –1
The two possible values of k are -1 and 4. The question asks us to find their sum, which is 3.
The answer is 3.
We are told that f(x) = x2 - 4x + 2, and g(x) = 6 - x. Let's find expressions for f(k) and g(k).
f(k) = k2 – 4k + 2
g(k) = 6 – k
Now, we can set these expressions equal.
f(k) = g(k)
k2 – 4k +2 = 6 – k
Add k to both sides.
k2 – 3k + 2 = 6
Then subtract 6 from both sides.
k2 – 3k – 4 = 0
Factor the quadratic equation. We must think of two numbers that multiply to give us -4 and that add to give us -3. These two numbers are –4 and 1.
(k – 4)(k + 1) = 0
Now we set each factor equal to 0 and solve for k.
k – 4 = 0
k = 4
k + 1 = 0
k = –1
The two possible values of k are -1 and 4. The question asks us to find their sum, which is 3.
The answer is 3.
Compare your answer with the correct one above
Which of the following is a solution to:

Which of the following is a solution to:
You may use the quadratic formula (where  ), which yields two answers,
), which yields two answers,  and
and  .
.
Since the only solution that appears in the answer list is  , we choose
, we choose  .
.
You may use the quadratic formula (where 


Since the only solution that appears in the answer list is 

Compare your answer with the correct one above
Solve for x: (x2 – x) / (x – 1) = 1
Solve for x: (x2 – x) / (x – 1) = 1
Begin by multiplying both sides by (x – 1):
x2 – x = x – 1
Solve as a quadratic equation: x2 – 2x + 1 = 0
Factor the left: (x – 1)(x – 1) = 0
Therefore, x = 1.
However, notice that in the original equation, a value of 1 for x would place a 0 in the denominator. Therefore, there is no solution.
Begin by multiplying both sides by (x – 1):
x2 – x = x – 1
Solve as a quadratic equation: x2 – 2x + 1 = 0
Factor the left: (x – 1)(x – 1) = 0
Therefore, x = 1.
However, notice that in the original equation, a value of 1 for x would place a 0 in the denominator. Therefore, there is no solution.
Compare your answer with the correct one above
If f(x) = -x2 + 6x - 5, then which could be the value of a if f(a) = f(1.5)?
If f(x) = -x2 + 6x - 5, then which could be the value of a if f(a) = f(1.5)?
We need to input 1.5 into our function, then we need to input "a" into our function and set these results equal.
f(a) = f(1.5)
f(a) = -(1.5)2 +6(1.5) -5
f(a) = -2.25 + 9 - 5
f(a) = 1.75
-a2 + 6a -5 = 1.75
Multiply both sides by 4, so that we can work with only whole numbers coefficients.
-4a2 + 24a - 20 = 7
Subtract 7 from both sides.
-4a2 + 24a - 27 = 0
Multiply both sides by negative one, just to make more positive coefficients, which are usually easier to work with.
4a2 - 24a + 27 = 0
In order to factor this, we need to mutiply the outer coefficients, which gives us 4(27) = 108. We need to think of two numbers that multiply to give us 108, but add to give us -24. These two numbers are -6 and -18. Now we rewrite the equation as:
4a2 - 6a -18a + 27 = 0
We can now group the first two terms and the last two terms, and then we can factor.
(4a2 - 6a )+(-18a + 27) = 0
2a(2a-3) + -9(2a - 3) = 0
(2a-9)(2a-3) = 0
This means that 2a - 9 =0, or 2a - 3 = 0.
2a - 9 = 0
2a = 9
a = 9/2 = 4.5
2a - 3 = 0
a = 3/2 = 1.5
So a can be either 1.5 or 4.5.
The only answer choice available that could be a is 4.5.
We need to input 1.5 into our function, then we need to input "a" into our function and set these results equal.
f(a) = f(1.5)
f(a) = -(1.5)2 +6(1.5) -5
f(a) = -2.25 + 9 - 5
f(a) = 1.75
-a2 + 6a -5 = 1.75
Multiply both sides by 4, so that we can work with only whole numbers coefficients.
-4a2 + 24a - 20 = 7
Subtract 7 from both sides.
-4a2 + 24a - 27 = 0
Multiply both sides by negative one, just to make more positive coefficients, which are usually easier to work with.
4a2 - 24a + 27 = 0
In order to factor this, we need to mutiply the outer coefficients, which gives us 4(27) = 108. We need to think of two numbers that multiply to give us 108, but add to give us -24. These two numbers are -6 and -18. Now we rewrite the equation as:
4a2 - 6a -18a + 27 = 0
We can now group the first two terms and the last two terms, and then we can factor.
(4a2 - 6a )+(-18a + 27) = 0
2a(2a-3) + -9(2a - 3) = 0
(2a-9)(2a-3) = 0
This means that 2a - 9 =0, or 2a - 3 = 0.
2a - 9 = 0
2a = 9
a = 9/2 = 4.5
2a - 3 = 0
a = 3/2 = 1.5
So a can be either 1.5 or 4.5.
The only answer choice available that could be a is 4.5.
Compare your answer with the correct one above
The height of a ball (in feet) after it is thrown in the air is given by the expression
s(t) = –t_2 + 4_t
where t is time in seconds. The ball is thrown from ground level at t = 0. How many seconds will pass before the ball reaches the ground again?
The height of a ball (in feet) after it is thrown in the air is given by the expression
s(t) = –t_2 + 4_t
where t is time in seconds. The ball is thrown from ground level at t = 0. How many seconds will pass before the ball reaches the ground again?
Notice that when the ball is at ground level, the height is zero. Setting s (t) equal to zero and solving for t will then give the times when the ball is at the ground.
–t_2 + 4_t =0
t(4 – t) = 0
t = 0, t = 4
The ball returns to the ground after 4 seconds.
Notice that when the ball is at ground level, the height is zero. Setting s (t) equal to zero and solving for t will then give the times when the ball is at the ground.
–t_2 + 4_t =0
t(4 – t) = 0
t = 0, t = 4
The ball returns to the ground after 4 seconds.
Compare your answer with the correct one above
The formula to solve a quadratic expression is:

All of the following equations have real solutions EXCEPT:
The formula to solve a quadratic expression is:
All of the following equations have real solutions EXCEPT:
We can use the quadratic formula to find the solutions to quadratic equations in the form ax2 + bx + c = 0. The quadratic formula is given below.

In order for the formula to give us real solutions, the value under the square root, b2 – 4ac, must be greater than or equal to zero. Otherwise, the formula will require us to find the square root of a negative number, which gives an imaginary (non-real) result.
In other words, we need to look at each equation and determine the value of b2 – 4ac. If the value of b2 – 4ac is negative, then this equation will not have real solutions.
Let's look at the equation 2x2 – 4x + 5 = 0 and determine the value of b2 – 4ac.
b2 – 4ac = (–4)2 – 4(2)(5) = 16 – 40 = –24 < 0
Because the value of b2 – 4ac is less than zero, this equation will not have real solutions. Our answer will be 2x2 – 4x + 5 = 0.
If we inspect all of the other answer choices, we will find positive values for b2 – 4ac, and thus these other equations will have real solutions.
We can use the quadratic formula to find the solutions to quadratic equations in the form ax2 + bx + c = 0. The quadratic formula is given below.
In order for the formula to give us real solutions, the value under the square root, b2 – 4ac, must be greater than or equal to zero. Otherwise, the formula will require us to find the square root of a negative number, which gives an imaginary (non-real) result.
In other words, we need to look at each equation and determine the value of b2 – 4ac. If the value of b2 – 4ac is negative, then this equation will not have real solutions.
Let's look at the equation 2x2 – 4x + 5 = 0 and determine the value of b2 – 4ac.
b2 – 4ac = (–4)2 – 4(2)(5) = 16 – 40 = –24 < 0
Because the value of b2 – 4ac is less than zero, this equation will not have real solutions. Our answer will be 2x2 – 4x + 5 = 0.
If we inspect all of the other answer choices, we will find positive values for b2 – 4ac, and thus these other equations will have real solutions.
Compare your answer with the correct one above
Find the solutions of this quadratic equation:
4y3 - 4y2 = 8y
Find the solutions of this quadratic equation:
4y3 - 4y2 = 8y
4y3 - 4y2 = 8y
Divide by y and set equal to zero.
4y2 - 4y – 8 = 0
(2y + 2)(2y – 4) = 0
2y + 2 = 0
2y = –2
y = –1
2y – 4 = 0
2y = 4
y = 2
4y3 - 4y2 = 8y
Divide by y and set equal to zero.
4y2 - 4y – 8 = 0
(2y + 2)(2y – 4) = 0
2y + 2 = 0
2y = –2
y = –1
2y – 4 = 0
2y = 4
y = 2
Compare your answer with the correct one above
3x2 – 11x = –10
Which of the following is a valid value for x?
3x2 – 11x = –10
Which of the following is a valid value for x?
Begin by getting our equation into the form Ax2 + BX + C = 0:
3x2 – 11x + 10 = 0
Now, if you factor the left, you can find the answer. Begin by considering the two groups. They will have to begin respectively with 3 and 1 as coefficients for your x value. Likewise, looking at the last element, you can tell that both will have to have a + or –, since the C coefficient is positive. Finally, since the B coefficient is negative, we know that it will have to be –. We know therefore:
(3x – ?)(x – ?)
The potential factors of 10 are: 10, 1; 1, 10; 2, 5; 5, 2
5 and 2 work:
(3x – 5)(x – 2) = 0 because you can FOIL (3x – 5)(x – 2) back into 3x2 – 11x + 10.
Now, the trick remaining is to set each of the factors equal to 0 because if either group is 0, the whole equation will be 0:
3x – 5 = 0 → 3x = 5 → x = 5/3
x – 2 = 0 → x = 2
Therefore, x is either 5 / 3 or 2. The former is presented as an answer.
Begin by getting our equation into the form Ax2 + BX + C = 0:
3x2 – 11x + 10 = 0
Now, if you factor the left, you can find the answer. Begin by considering the two groups. They will have to begin respectively with 3 and 1 as coefficients for your x value. Likewise, looking at the last element, you can tell that both will have to have a + or –, since the C coefficient is positive. Finally, since the B coefficient is negative, we know that it will have to be –. We know therefore:
(3x – ?)(x – ?)
The potential factors of 10 are: 10, 1; 1, 10; 2, 5; 5, 2
5 and 2 work:
(3x – 5)(x – 2) = 0 because you can FOIL (3x – 5)(x – 2) back into 3x2 – 11x + 10.
Now, the trick remaining is to set each of the factors equal to 0 because if either group is 0, the whole equation will be 0:
3x – 5 = 0 → 3x = 5 → x = 5/3
x – 2 = 0 → x = 2
Therefore, x is either 5 / 3 or 2. The former is presented as an answer.
Compare your answer with the correct one above
Which of the following is the closest approximate solution for x where 11x2 – 7x – 8 = 0?
Which of the following is the closest approximate solution for x where 11x2 – 7x – 8 = 0?
Apply the quadratic formula directly to get \[7 ± (49 – 4 * 11 * –8)0.5\]/22, → \[7 ± (≈ 20)\]/22
So our approximate answers are 27/22 and –13/22, and 27/22 is our answer.
Apply the quadratic formula directly to get \[7 ± (49 – 4 * 11 * –8)0.5\]/22, → \[7 ± (≈ 20)\]/22
So our approximate answers are 27/22 and –13/22, and 27/22 is our answer.
Compare your answer with the correct one above
What is the sum of the values of x that satisfy the following equation:
16x – 10(4)x + 16 = 0.
What is the sum of the values of x that satisfy the following equation:
16x – 10(4)x + 16 = 0.
The equation we are asked to solve is 16x – 10(4)x + 16 = 0.
Equations of this type can often be "transformed" into other equations, such as linear or quadratic equations, if we rewrite some of the terms.
First, we can notice that 16 = 42. Thus, we can write 16x as (42)x or as (4x)2.
Now, the equation is (4x)2 – 10(4)x + 16 = 0
Let's introduce the variable u, and set it equal 4x. The advantage of this is that it allows us to "transform" the original equation into a quadratic equation.
u2 – 10u + 16 = 0
This is an equation with which we are much more familiar. In order to solve it, we need to factor it and set each factor equal to zero. In order to factor it, we must think of two numbers that multiply to give us 16 and add to give us –10. These two numbers are –8 and –2. Thus, we can factor u2 – 10u + 16 = 0 as follows:
(u – 8)(u – 2) = 0
Next, we set each factor equal to 0.
u – 8 = 0
Add 8.
u = 8
u – 2 = 0
Add 2.
u = 2.
Thus, u must equal 2 or 8. However, we want to find x, not u. Since we defined u as equal to 4x, the equations become:
4x = 2 or 4x = 8
Let's solve 4x = 2 first. We can rewrite 4x as (22)x = 22x, so that the bases are the same.
22x = 2 = 21
2x = 1
x = 1/2
Finally, we will solve 4x = 8. Once again, let's write 4x as 22x. We can also write 8 as 23.
22x = 23
2x = 3
x = 3/2
The original question asks us to find the sum of the values of x that solve the equation. Because x can be 1/2 or 3/2, the sum of 1/2 and 3/2 is 2.
The answer is 2.
The equation we are asked to solve is 16x – 10(4)x + 16 = 0.
Equations of this type can often be "transformed" into other equations, such as linear or quadratic equations, if we rewrite some of the terms.
First, we can notice that 16 = 42. Thus, we can write 16x as (42)x or as (4x)2.
Now, the equation is (4x)2 – 10(4)x + 16 = 0
Let's introduce the variable u, and set it equal 4x. The advantage of this is that it allows us to "transform" the original equation into a quadratic equation.
u2 – 10u + 16 = 0
This is an equation with which we are much more familiar. In order to solve it, we need to factor it and set each factor equal to zero. In order to factor it, we must think of two numbers that multiply to give us 16 and add to give us –10. These two numbers are –8 and –2. Thus, we can factor u2 – 10u + 16 = 0 as follows:
(u – 8)(u – 2) = 0
Next, we set each factor equal to 0.
u – 8 = 0
Add 8.
u = 8
u – 2 = 0
Add 2.
u = 2.
Thus, u must equal 2 or 8. However, we want to find x, not u. Since we defined u as equal to 4x, the equations become:
4x = 2 or 4x = 8
Let's solve 4x = 2 first. We can rewrite 4x as (22)x = 22x, so that the bases are the same.
22x = 2 = 21
2x = 1
x = 1/2
Finally, we will solve 4x = 8. Once again, let's write 4x as 22x. We can also write 8 as 23.
22x = 23
2x = 3
x = 3/2
The original question asks us to find the sum of the values of x that solve the equation. Because x can be 1/2 or 3/2, the sum of 1/2 and 3/2 is 2.
The answer is 2.
Compare your answer with the correct one above
2_x_ + _y_3 + _xy_2 + y = x
If y = 1, what is x?
2_x_ + _y_3 + _xy_2 + y = x
If y = 1, what is x?
Plug in y = 1. Then solve for x.
2_x_ + _y_3 + _xy_2 + y = x
2_x_ + 1 + x + 1 = x
3x + 2 = x
2x = -2
x = -1
Plug in y = 1. Then solve for x.
2_x_ + _y_3 + _xy_2 + y = x
2_x_ + 1 + x + 1 = x
3x + 2 = x
2x = -2
x = -1
Compare your answer with the correct one above
I. real
II. rational
III. distinct
Which of the descriptions characterizes the solutions of the equation 2x2 – 6x + 3 = 0?
I. real
II. rational
III. distinct
Which of the descriptions characterizes the solutions of the equation 2x2 – 6x + 3 = 0?
The equation in the problem is quadratic, so we can use the quadratic formula to solve it. If an equation is in the form _ax_2 + bx + c = 0, where a, b, and c are constants, then the quadratic formula, given below, gives us the solutions of x.
![]()
In this particular problem, a = 2, b = –6, and c = 3.
The value under the square-root, b_2 – 4_ac, is called the discriminant, and it gives us important information about the nature of the solutions of a quadratic equation.
If the discriminant is less than zero, then the roots are not real, because we would be forced to take the square root of a negative number, which yields an imaginary result. The discriminant of the equation we are given is (–6)2 – 4(2)(3) = 36 – 24 = 12 > 0. Because the discriminant is not negative, the solutions to the equation will be real. Thus, option I is correct.
The discriminant can also tell us whether the solutions of an equation are rational or not. If we take the square root of the discriminant and get a rational number, then the solutions of the equation must be rational. In this problem, we would need to take the square root of 12. However, 12 is not a perfect square, so taking its square root would produce an irrational number. Therefore, the solutions to the equation in the problem cannot be rational. This means that choice II is incorrect.
Lastly, the discriminant tells us if the roots to an equation are distinct (different from one another). If the discriminant is equal to zero, then the solutions of x become (–b + 0)/2_a_ and (–b – 0)/2_a_, because the square root of zero is 0. Notice that (–b + 0)/2_a_ is the same as (–b – 0)/2_a_. Thus, if the discriminant is zero, then the roots of the equation are the same, i.e. indistinct. In this particular problem, the discriminant = 12, which doesn't equal zero. This means that the two roots will be different, i.e. distinct. Therefore, choice III applies.
The answer is choices I and III only.
The equation in the problem is quadratic, so we can use the quadratic formula to solve it. If an equation is in the form _ax_2 + bx + c = 0, where a, b, and c are constants, then the quadratic formula, given below, gives us the solutions of x.
In this particular problem, a = 2, b = –6, and c = 3.
The value under the square-root, b_2 – 4_ac, is called the discriminant, and it gives us important information about the nature of the solutions of a quadratic equation.
If the discriminant is less than zero, then the roots are not real, because we would be forced to take the square root of a negative number, which yields an imaginary result. The discriminant of the equation we are given is (–6)2 – 4(2)(3) = 36 – 24 = 12 > 0. Because the discriminant is not negative, the solutions to the equation will be real. Thus, option I is correct.
The discriminant can also tell us whether the solutions of an equation are rational or not. If we take the square root of the discriminant and get a rational number, then the solutions of the equation must be rational. In this problem, we would need to take the square root of 12. However, 12 is not a perfect square, so taking its square root would produce an irrational number. Therefore, the solutions to the equation in the problem cannot be rational. This means that choice II is incorrect.
Lastly, the discriminant tells us if the roots to an equation are distinct (different from one another). If the discriminant is equal to zero, then the solutions of x become (–b + 0)/2_a_ and (–b – 0)/2_a_, because the square root of zero is 0. Notice that (–b + 0)/2_a_ is the same as (–b – 0)/2_a_. Thus, if the discriminant is zero, then the roots of the equation are the same, i.e. indistinct. In this particular problem, the discriminant = 12, which doesn't equal zero. This means that the two roots will be different, i.e. distinct. Therefore, choice III applies.
The answer is choices I and III only.
Compare your answer with the correct one above
Solve for x.
3_x_2 + 15_x_ – 18 = 0.
Solve for x.
3_x_2 + 15_x_ – 18 = 0.
First let's see if there is a common term.
3_x_2 + 15_x_ – 18 = 0
We can pull out a 3: 3(x_2 + 5_x – 6) = 0
Divide both sides by 3: x_2 + 5_x – 6 = 0
We need two numbers that sum to 5 and multiply to –6. 6 and –1 work.
(x + 6)(x – 1) = 0
x = –6 or x = 1
First let's see if there is a common term.
3_x_2 + 15_x_ – 18 = 0
We can pull out a 3: 3(x_2 + 5_x – 6) = 0
Divide both sides by 3: x_2 + 5_x – 6 = 0
We need two numbers that sum to 5 and multiply to –6. 6 and –1 work.
(x + 6)(x – 1) = 0
x = –6 or x = 1
Compare your answer with the correct one above