How to find the domain of a function - ACT Math
Card 0 of 12
Which of the following represents the domain of 
where:
Which of the following represents the domain of
Using our properties of exponents, we could rewrite 
as 
This means that when we input 
, we first subtract 2, then take this to the fourth power, then take the fifth root, and then add three. We want to look at these steps individually and see whether there are any values that wouldn’t work at each step. In other words, we want to know which 
values we can put into our function at each step without encountering any problems.
The first step is to subtract 2 from 
. The second step is to take that result and raise it to the fourth power. We can subtract two from any number, and we can take any number to the fourth power, which means that these steps don't put any restrictions on 
.
Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function 
is defined for any value of 
; thus the fact that 
has a fifth root in it doesn't put any restrictions on 
, because we can add three to any number; therefore, the domain for 
is all real values of 
.
Using our properties of exponents, we could rewrite
This means that when we input
The first step is to subtract 2 from
Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function
Compare your answer with the correct one above
Find the domain of the function:
Find the domain of the function:
If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into
and then cancelling the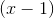 
from the numerator and the denominator.
This new expression, 
is the equation of the function, but it will have a hole at the point where the denominator originally would have been zero. Thus, this graph will look like the line 
with a hole where 
, which is
.
Thus the domain of the function is all 
values such that 
If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into
and then cancelling the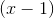
This new expression,
Thus the domain of the function is all
Compare your answer with the correct one above
What is the domain of the given function?
What is the domain of the given function?
The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.
The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.
Compare your answer with the correct one above
Find the domain of the given function:
Find the domain of the given function:
When x = 0 or x = 3, the function is undefined due to its denominator.
Thus the domain is all real numbers x, such that x is not equal to 0 or 3.
When x = 0 or x = 3, the function is undefined due to its denominator.
Thus the domain is all real numbers x, such that x is not equal to 0 or 3.
Compare your answer with the correct one above
Which of the following represents the domain of the function 
?
Which of the following represents the domain of the function
You know that the square root function has real roots only for positive values. Therefore, you know that 
. From this, you can solve for your domain:
You know that the square root function has real roots only for positive values. Therefore, you know that
Compare your answer with the correct one above
Which of the following represents the domain of the function 
?
Which of the following represents the domain of the function
For this function, the only thing to which you need to pay heed is the denominator of the fraction, which cannot be equal to zero. Thus, you can just look at the polynomial found in the denominator and solve for the values of 
equal to 
This is solved by factoring:
This indicates that 
Otherwise, all values are fine!
For this function, the only thing to which you need to pay heed is the denominator of the fraction, which cannot be equal to zero. Thus, you can just look at the polynomial found in the denominator and solve for the values of
This is solved by factoring:
This indicates that
Otherwise, all values are fine!
Compare your answer with the correct one above
What is the domain of the function defined as follows:
What is the domain of the function defined as follows:
The domain is the set of all 
where the function is defined. Since we can't divide by 0, we need to find the 
values that would make the denominator zero. Set the denominator equal to zero and solve for 
to find:
Thus 
can take all values except for positive and negative 2, so the domain is:
The domain is the set of all
Thus
Compare your answer with the correct one above
What is the domain of 
?
What is the domain of
The domain of the function 
is 
, because the result of taking the square root of a negative number is imaginary.
Therefore, for the function given, 
, 
when 
.
So the domain must be 
.
The domain of the function
Therefore, for the function given,
So the domain must be
Compare your answer with the correct one above
What is the domain of 
?
What is the domain of
To find the domain we want to find any areas for which an x value will not work in our function. The potential problem area would be that under the radical.
Therefore, for the function given, 
, 
for all real numbers 
.
So the domain must be 
.
In other words, there is no real value of 
whose absolute value is less than 
let alone 
To find the domain we want to find any areas for which an x value will not work in our function. The potential problem area would be that under the radical.
Therefore, for the function given,
So the domain must be
In other words, there is no real value of
Compare your answer with the correct one above
What is the domain of the following function?
What is the domain of the following function?
Looking at our numerator shows us that 
can never be negative, as it would result in a nonreal solution for the numerator. The denominator solves to a real value for all positive integers until 
, where it causes us to divide by zero, and all numbers past 
result in a negative radical (and thus a nonreal solution) for the denominator.
Testing 
itself produces 
, which is a fine answer. Therefore, our domain is inclusive of 
and exclusive of 
, and should be written as 
.
Looking at our numerator shows us that
Testing
Compare your answer with the correct one above
What is the domain of the following function?
What is the domain of the following function?
The two potential concerns for domain in a standard function are negative numbers inside even-powered radicals, and dividing by zero. In this case, the radical we have is odd-powered, so having a negative result underneath the radical is fine. All we need to do, then, is avoid dividing by zero, which means avoiding a result which sums to zero under the radical. In this case, only 
will create this situation, so we must avoid it.
Thus, our domain is 
The two potential concerns for domain in a standard function are negative numbers inside even-powered radicals, and dividing by zero. In this case, the radical we have is odd-powered, so having a negative result underneath the radical is fine. All we need to do, then, is avoid dividing by zero, which means avoiding a result which sums to zero under the radical. In this case, only
Thus, our domain is
Compare your answer with the correct one above
Find the domain of the following function:
Find the domain of the following function:
To find the domain, you must find the values for which you can plug in for 
. Based on the given function, you know that you can not have a demoninator equal to 
. So, by setting the denominator equal to 
, you can find out the values that can not be in the domain, and then simply remove them from your set of numbers from negative infinity to positive infinity.
Thus,
Therefore, for our function, 
can not equal 
or it will be undefined. Thus, we get the set of numbers excluding positive 
.
To find the domain, you must find the values for which you can plug in for
Thus,
Therefore, for our function,
Compare your answer with the correct one above