Solid Geometry - ACT Math

Card 0 of 20

Question

Find the length of the diagonal of a cube with side length of .

Answer

We begin with a picture, noting that the diagonal, labeled as , is the length across the cube from one vertex to the opposite side's vertex.

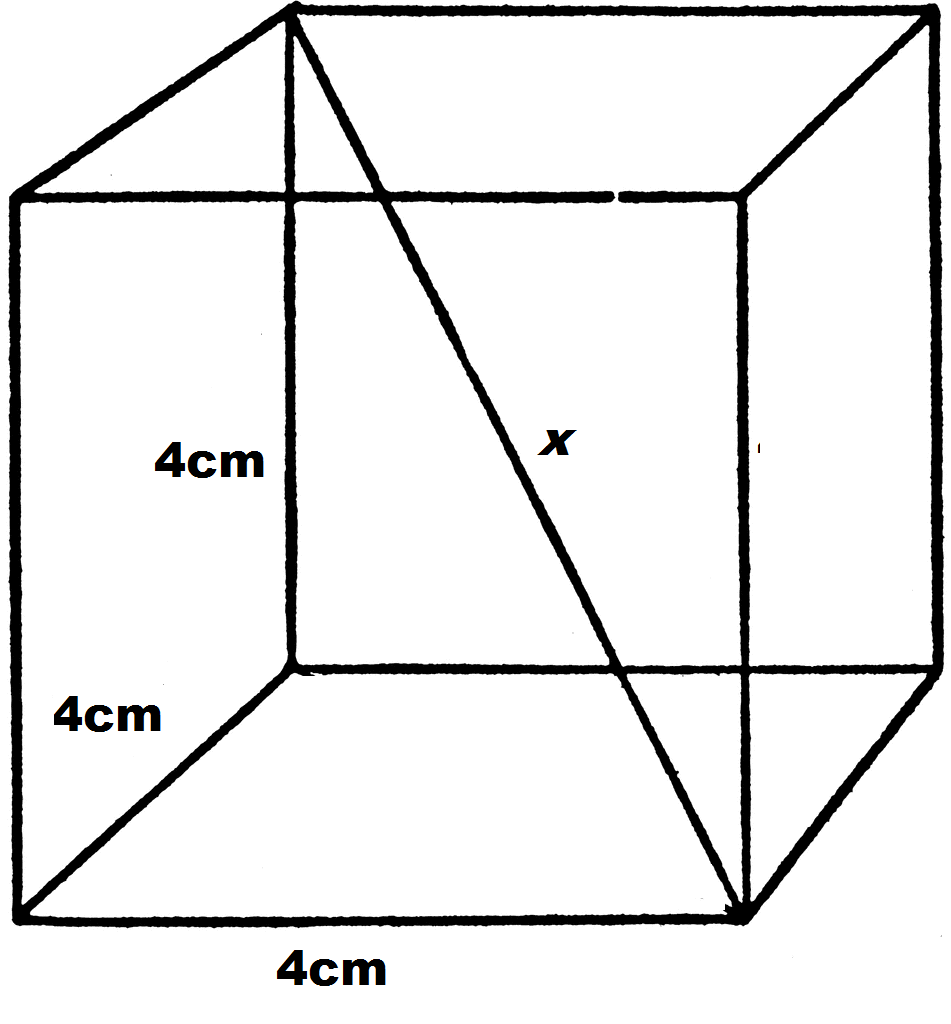
However, the trick to solving the problem is to also draw in the diagonal of the bottom face of the cube, which we labeled .

Note that this creates two right triangles. Though our end goal is to find , we can begin by looking at the right triangle in the bottom face to find . Using either the Pythagorean Theorem or the fact that we have a 45-45-90 right traingle, we can calculate the hypotenuse.

$y=4\sqrt{2}$

Now that we know the value of , we can turn to our second right triangle to find using the Pythagorean Theorem.

$(4)^2+(4\sqrt{2})^2=x^2$

Taking the square root of both sides and simplifying gives the answer.

$x=4\sqrt{3}cm$

Compare your answer with the correct one above

Question

What is the diagonal length for a cube with volume of ? Round to the nearest hundredth.

Answer

Recall that the volume of a cube is computed using the equation

, where is the length of one side of the cube.

So, for our data, we know:

Using your calculator, take the cube root of both sides. You can always do this by raising to the $\frac{1}{3}$ power if your calculator does not have a varied-root button.

$\sqrt[3]{91.125} = \sqrt[3]{s^3}$

If you get , the value really should be rounded up to . This is because of calculator estimations. So, if the sides are , you can find the diagonal by using a variation on the Pythagorean Theorem working for three dimensions:

$diagonal=\sqrt{s^2+s^2+s^2}$

$diagonal = \sqrt{4.5^2+4.5^2+4.5^2}=\sqrt{60.75}$

This is . Round it to .

Compare your answer with the correct one above

Question

What is the length of the diagonal of a cube with a volume of ?

Answer

Recall that the diagonal of a cube is most easily found when you know that cube's dimensions. For the volume of a cube, the pertinent equation is:

, where represents the length of one side of the cube. For our data, this gives us:

Now, you could factor this by hand or use your calculator. You will see that is .

Now, we find the diagonal by using a three-dimensional version of the Pythagorean Theorem / distance formula:

$d = \sqrt{33^2+33^2+33^2}$ or $d=\sqrt{3*33^2}$

You can rewrite this:

$d=33\sqrt{3}$

Compare your answer with the correct one above

Question

A right, rectangular prism has has a length of , a width of , and a height of . What is the length of the diagonal of the prism?

Answer

First we must find the diagonal of the prism's base ( $\small d$ ). This can be done by using the Pythagorean Theorem with the length ( $\small l$ ) and width ( $\small w$ ):

$\small l^2+w^2=d^2$

$\small 6^2+9^2=d^2$

$\small 36+81=d^2$

$\small 117=d^2$

$\small d=\sqrt{117}$

Therefore, the diagonal of the prism's base is $\small \sqrt{117}cm$ . We can then use this again in the Pythagorean Theorem, along with the height of the prism ( $\small h$ ), to find the diagonal of the prism ( $\small D$ ):

$\small d^2+h^2=D^2$

$\small (\sqrt{117})^2+12^2=D^2$

$\small 117+144=D^2$

$\small D^2=261$

$\small D=\sqrt{261}=\sqrt{9}\sqrt{29}=3\sqrt{29}$

Therefore, the length of the prism's diagonal is $\small 3\sqrt{29}cm$ .

Compare your answer with the correct one above

Question

What is the diagonal of a rectangular prism with a height of 4, width of 4 and height of 6?

Answer

In order to solve this problem, it's helpful to visualize where the diagonal is within the prism.

In this image, the diagonal is the pink line. By noting how it relates to the blue and green lines, we can observe how the pink line is connected and creates a right triangle. This very quickly becomes a problem that employs the Pythagorean theorem.

The goal is essentially to find the hypotenuse of this sketched-in right triangle; however, only one of the legs is given: the green line, the height of the prism. The blue line can be solved for by understanding that it is the measurement of the diagonal of a 4x4 square.

Either using trig functions or the rules for a special 45/45/90 triangle, the blue line measures out to be $4\sqrt2$ .

The rules for a 45/45/90 triangle: both legs are "" and the hypotenuse is " $s\sqrt2$ ". Keep in mind, this is is only for isosceles right triangles.

Now that both legs are known, we can solve for the hypotenuse (diagonal).

$(4\sqrt{2})^2+(6)^2=c^2$

$\sqrt{68}=c$

${\color{Blue} 8.2}=c$

Compare your answer with the correct one above

Question

Find the diagonal of a right rectangular prism if the length, width, and height are 3,4, and 5, respectively.

Answer

Write the diagonal formula for a rectangular prism.

$d=\sqrt{L^2+W^2+H^2}$

Substitute and solve for the diagonal.

$d=\sqrt{3^2+4^2+5^2}= \sqrt{9+16+25}= \sqrt{50}= 5\sqrt2$

Compare your answer with the correct one above

Question

If the dimensions of a right rectangular prism are 1 yard by 1 foot by 1 inch, what is the diagonal in feet?

Answer

Convert the dimensions into feet.

$1 \textup{ yard}= 3\textup{ feet}$

$\textup{1 inch }= \frac{1}{12}\textup{ foot}$

The new dimensions of rectangular prism in feet are: $3\times1\times \frac{1}{12}$

Write the formula for the diagonal of a right rectangular prism and substitute.

$d=\sqrt{L^2+W^2+H^2}$

$d=\sqrt{3^2+1^2+\frac{1}{12}^2}=\sqrt{9+1+\frac{1}{144}}=\sqrt{\frac{1440}{144}+\frac{1}{144}}$

$d=\sqrt{\frac{1441}{144}} =\frac{\sqrt{1441}}{12}\textup{ ft}$

Compare your answer with the correct one above

Question

Calculate the diagonal of a regular tetrahedron (all of the faces are equilateral triangles) with side length .

Answer

The diagonal of a shape is simply the length from a vertex to the center of the face or vertex opposite to it. With a regular tetrahedron, we have a face opposite to the vertex, and this basically amounts to calculating the height of our shape.

We know that the height of a tetrahedron is ${\large }s\sqrt{\frac{2}{3}}$ where s is the side length, so we can put into this formula:

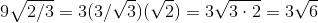
${\large} 9\sqrt{2/3} = 3(3/\sqrt3)(\sqrt2) = 3\sqrt{3\cdot2} = 3\sqrt{6}$

which gives us the correct answer.

Compare your answer with the correct one above

Question

If a sphere has a volume of $36\pi$ , what is its diameter?

Answer

1. Use the volume to find the radius:

$Volume=\frac{4}{3}\pi r^{3}$

$36\pi = \frac{4}{3}\pi r^{3}$

$\frac{3}{4}(36\pi) = (\frac{4}{3}\pi r^{3})\frac{3}{4}$

$27=r^{3}$

2. Use the radius to find the diameter:

$d=2r=2\cdot 3=6$

Compare your answer with the correct one above

Question

A sphere has a volume of $36\pi$ . What is its diameter?

Answer

This question relies on knowledge of the formula for volume of a sphere, which is as follows: $V=\frac{4}{3}\pi r^{3}}$

In this equation, we have two variables, and . Additionally, we know that $V=36\pi$ and is unknown. You can begin by rearranging the volume equation so it is solved for , then plug in and solve for :

Rearranged form:

$r=\sqrt[3]{\frac{3}{4\pi}V}$

Plug in $36\pi$ for V

$r=\sqrt[3]{\frac{3}{4\pi}36\pi}$

Simplify the part under the cubed root

Cancel the $\pi$ 's since they are in the numerator and denominator.

Simplify the fraction and the :

$36*\frac{3}{4}=27$

Thus we are left with

$r=\sqrt[3]{27}$

Then, either use your calculator and enter $27^{\frac{1}{3}}$ Or recall that $3^{3}=27$ in order to find that .

We're almost there, but we need to go a step further. Dodge the trap answer "" and carry on. Read the question carefully to see that we need the diameter, not the radius.

So

is our final answer.

Compare your answer with the correct one above

Question

A spherical plastic ball has a diameter of . What is the volume of the ball to the nearest cubic inch?

Answer

To answer this question, we must calculate the volume of the ball using the equation for the volume of a sphere. The equation for the volume of a sphere is four-thirds multiplied by pi, which is then multiplied by the radius cubed. The equation can be written like this:

$V = \frac{4}{3}\pi r^{3}$

We are given the diameter of the sphere in the problem, which is . To get the radius from the diameter, we divide the diameter by . So, for this data:

$radius=\frac{diameter}{2}=\frac{4}{2}=2$

We can then plug our newly found radius of two into the equation to find the volume. For this data:

$Volume = \frac{4}{3}\pi r^{3}=\frac{4}{3}\pi \cdot (2)^{3} = \frac{4}{3}\pi\cdot 8$

We then multiply $\frac{4}{3}$ by .

$\frac{4}{3}\pi\cdot 8=\frac{32}{3}\pi$

We finally substitute 3.14 for pi and multiply again to get our answer.

$\frac{32}{3}\pi = 33.5$

The question asked us to round to the nearest whole cubic inch. To do this, we round a number up one place if the last digit is a 5, 6, 7, 8, or 9, and we round it down if the last digit is a 1, 2, 3, or 4. Therefore:

$33.5\rightarrow34$

Therefore our answer is .

Compare your answer with the correct one above

Question

A boulder breaks free on a slope and rolls downhill. It rolls for complete revolutions before grinding to a halt. If the boulder has a volume of cubic feet, how far in feet did the boulder roll? (Assume the boulder doesn't lose mass to friction). Round $\pi$ to 3 significant digits. Round your final answer to the nearest integer.

Answer

The formula for the volume of a sphere is:

$V = \frac{4}{3}\pi r^3$

To figure out how far the sphere rolled, we need to know the circumference, so we must first figure out radius. Solve the formula for volume in terms of radius:

$1436 = \frac{4}{3}\pi r^3$

$\frac{1077}{\pi} =r^3$

$r \approx 6.999932$

Since the answer asks us to round to the nearest integer, we are safe to round to at this point.

To find circumference, we now apply our circumference formula:

$C = 2r\pi = 14\pi$

If our boulder rolled times, it covered that many times its own circumference.

$355\cdot 14\pi = 4970\pi \approx 15606$

Thus, our boulder rolled for

Compare your answer with the correct one above

Question

Find the diameter of a sphere whose radius is .

Answer

To solve, simply remember that diameter is twice the radius. Don't be fooled when the radius is an algebraic expression and incorporates the arbitrary constant . Thus,

$\textup{diameter}=2r=2*2d=4d$

Compare your answer with the correct one above

Question

Our backyard pool holds 10,000 gallons. Its average depth is 4 feet deep and it is 10 feet long. If there are 7.48 gallons in a cubic foot, how wide is the pool?

Answer

There are 7.48 gallons in cubic foot. Set up a ratio:

1 ft3 / 7.48 gallons = x cubic feet / 10,000 gallons

Pool Volume = 10,000 gallons = 10,000 gallons * (1 ft3/ 7.48 gallons) = 1336.9 ft3

Pool Volume = 4ft x 10 ft x WIDTH = 1336.9 cubic feet

Solve for WIDTH:

4 ft x 10 ft x WIDTH = 1336.9 cubic feet

WIDTH = 1336.9 / (4 x 10) = 33.4 ft

Compare your answer with the correct one above

Question

A cube has a volume of 64cm3. What is the area of one side of the cube?

Answer

The cube has a volume of 64cm3, making the length of one edge 4cm (4 * 4 * 4 = 64).

So the area of one side is 4 * 4 = 16cm2

Compare your answer with the correct one above

Question

A cube as the volume of .

Find the length of a side of this cube.

Answer

The formula to find the volume of the cube is

Since we know the volume, we can set up the equation

$\sqrt[3]64=4$

Compare your answer with the correct one above

Question

A cube has a surface area of $1014\textup{ in}^2$ , what is the length of the side of the cube? (If necessary, round to the nearest hundredth.)

Answer

To find the length of the side of a square given the surface area, use the surface area formula and solve for :

$1014\textup{ inches}^2 = 6*s^2$ , now divide both sides by 6
$169\textup{ inches}^2 = s^2$ , now square root both sides
.

Compare your answer with the correct one above

Question

A certain cubic box when unfolded and laid flat on a table covers exactly square units of space. What is the width of the box, in units?

Answer

To find the length of the edge of a cube from its surface area, remember that $SA\square = 6s^2$ , where is the length of a side.

$s = \sqrt{60} = 2\sqrt{15}$

So, the box is $2\sqrt{15}$ units long.

Compare your answer with the correct one above

Question

Given the volume of a cube is , find the side length.

Answer

To find side length, simply realize that volume is the side length cubed. Thus,

$s=\sqrt[3]{V}=\sqrt[3]{64}=\sqrt[3]{4^3}=4$

Compare your answer with the correct one above

Question

Find the length of the edge of a cube given the volume is .

Answer

To solve, simply take the cube root of the volume. Thus,

$s=\sqrt[3]{V}=\sqrt[3]{27}=3$

Compare your answer with the correct one above

Tap the card to reveal the answer