Plane Geometry - ACT Math
Card 0 of 20
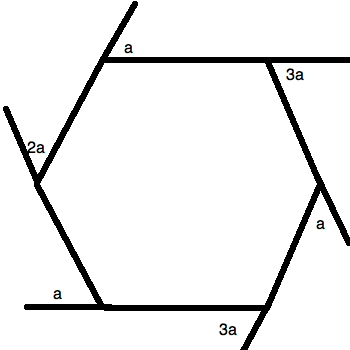
All of the angles marked are exterior angles.
What is the value of 
in degrees? Round to the nearest hundredth.
All of the angles marked are exterior angles.
What is the value of
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
, where 
is the number of sides.
Therefore, a hexagon like this one has:
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
. Since there are 
angles, you know that the numeric portion will be 
or 
. Thus, you can write:
Simplify and solve for 
:
This is 
or 
.
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
Therefore, a hexagon like this one has:
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to
Simplify and solve for
This is
Compare your answer with the correct one above
The sum of all the angles inside of a regular hexagon is 
. Determine the value of one angle.
The sum of all the angles inside of a regular hexagon is
In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to 
. To find the value of one angle, we must divide 
by 
, since there are 
angles inside of a hexagon.
In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to
Compare your answer with the correct one above
The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of 
?
The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
, where 
is the number of sides.
Therefore, a hexagon like this one has:
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
. Thus, you can write:
Solve for 
:
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
Therefore, a hexagon like this one has:
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to
Solve for
Compare your answer with the correct one above
If the diagonals of the quadrilateral above were drawn in the figure, they would form four 90 degree angles at the center. In degrees, what is the value of 
?
If the diagonals of the quadrilateral above were drawn in the figure, they would form four 90 degree angles at the center. In degrees, what is the value of
A quadrilateral is considered a kite when one of the following is true:
(1) it has two disjoint pairs of sides are equal in length or
(2) one diagonal is the perpendicular bisector of the other diagonal. Given the information in the question, we know (2) is definitely true.
To find 
we must first find the values of all of the angles.
The sum of angles within any quadrilateral is 360 degrees.
Therefore 
.
To find 
:
A quadrilateral is considered a kite when one of the following is true:
(1) it has two disjoint pairs of sides are equal in length or
(2) one diagonal is the perpendicular bisector of the other diagonal. Given the information in the question, we know (2) is definitely true.
To find
The sum of angles within any quadrilateral is 360 degrees.
Therefore
To find
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where 
is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: 
degrees 
degrees 
degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between 
degrees and the non-congruent opposite angles sum by 
:
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
Using the kite shown above, find the sum of the two remaining congruent interior angles.
Using the kite shown above, find the sum of the two remaining congruent interior angles.
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
Thus, 
degrees is the sum of the remaining two opposite angles.
Check:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
Thus,
Check:
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
Using the kite shown above, find the sum of the two remaining congruent interior angles.
Using the kite shown above, find the sum of the two remaining congruent interior angles.
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
Thus, 
degrees is the sum of the remaining two opposite angles.
The sum of the interior angles of any polygon can be found by applying the formula:
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
Thus,
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement of the sum of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
This means that 
degrees is the sum of the remaining two opposite angles and that each have an individual measurement of 
degrees.
Check:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
This means that
Check:
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement of the sum of the two remaining interior angles.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
This means that 
degrees is the sum of the remaining two opposite angles.
Check:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
This means that
Check:
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
Using the kite shown above, find the sum of the two remaining congruent interior angles.
Using the kite shown above, find the sum of the two remaining congruent interior angles.
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
degrees
Thus, 
degrees is the sum of the remaining two opposite angles.
The sum of the interior angles of any polygon can be found by applying the formula:
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
Thus,
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement of the sum of the two remaining interior angles.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
This means that 
is the sum of the remaining two opposite angles.
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
This means that
Compare your answer with the correct one above
In a particular kite, one angle that lies between congruent sides measures 
, and one angle that lies between non-congruent sides measures 
. What is the measure of the angle opposite the 
angle?
In a particular kite, one angle that lies between congruent sides measures
One of the rules governing kites is that the angles which lie between non-congruent sides are congruent to each other. Thus, we know one of the missing angles is also 
. Since all angles in a quadrilateral must sum to 
, we know that the other missing angle is
One of the rules governing kites is that the angles which lie between non-congruent sides are congruent to each other. Thus, we know one of the missing angles is also
Compare your answer with the correct one above
In the parallellogram, what is the value of 
?
In the parallellogram, what is the value of
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Compare your answer with the correct one above
In parallelogram 
, 
. What is 
In parallelogram
In the above parallelogram, 
and 
are consecutive angles (i.e. next to each other). In a parallelogram, consecutive angles are supplementary, meaning they add to 
.
In the above parallelogram,
Compare your answer with the correct one above
In parallelogram 
, 
. What is 
?
In parallelogram
In parallelogram 
, 
and 
are opposite angles. In a parallelogram, opposite angles are congruent. This means these two angles are equal.
In parallelogram
Compare your answer with the correct one above