Geometry - ACT Math
Card 0 of 20
A deer walks in a straight line for 8 hours. At the end of its journey, the deer is 30 miles north and 40 miles east of where it began. What was the average speed of the deer?
A deer walks in a straight line for 8 hours. At the end of its journey, the deer is 30 miles north and 40 miles east of where it began. What was the average speed of the deer?
To find the speed of the deer, you must have the distance traveled and the time.
The distance is found using the Pythagorean Theorem:
The answer must be in miles per hour so the total miles are divided by the hours to get the final answer:
To find the speed of the deer, you must have the distance traveled and the time.
The distance is found using the Pythagorean Theorem:
The answer must be in miles per hour so the total miles are divided by the hours to get the final answer:
Compare your answer with the correct one above
What is the slope of the line given by the equation 
?
What is the slope of the line given by the equation
To find the slope, put the line in slope intercept form. In other words put the equation in 
form where 
represents the slope and 
represents the y-intercept.
From here we can see our slope equals 
:
To find the slope, put the line in slope intercept form. In other words put the equation in
From here we can see our slope equals
Compare your answer with the correct one above
Find the distance between 
and 
Find the distance between
The expression used in solving this question is the distance formula: 
This formula is simply a variation of the Pythagorian Theorem. A great way to remember this formula is to visualize a right triangle where two of the vertices are the points given in the problem statement. For this question: 
Where a = 
and b = 
. Now it should be easy to see how the distance formula is simply a variation of the Pythagorean Theorem.
We almost have all of the information we need to solve the problem, but we still need to find the coordinates of the triangle at the right angle. This can be done by simply taking the y-coordinate of the first point and the x-coordinate of the second point, resulting in 
.
Now we can simply plug and chug using the distance formula. 
The expression used in solving this question is the distance formula:
This formula is simply a variation of the Pythagorian Theorem. A great way to remember this formula is to visualize a right triangle where two of the vertices are the points given in the problem statement. For this question:
Where a =
We almost have all of the information we need to solve the problem, but we still need to find the coordinates of the triangle at the right angle. This can be done by simply taking the y-coordinate of the first point and the x-coordinate of the second point, resulting in
Now we can simply plug and chug using the distance formula.
Compare your answer with the correct one above
Which point satisfies the system 
and 
Which point satisfies the system
In order to solve this problem, we need to find a point that will satisfy both equations. In order to do this, we need to combine the two equations into a single expression. For this, we need to isolate either x or y in one of the equations. Since the equation 
already has y isolated, we will use this equation. Next we substitue this equation into the first one. 
becomes 
which simplifies to 
. Now we can solve for x by factoring: 
Thus, 
.
Now that we have two possible values for x, we can plug each value into either equation to obtain two values for y. For 
and the second equation, we get 
. Therefore our first point is 
. This is not one of the listed answers, so we will use our other value of x. For 
and the second equation, we get 
. This gives us the point 
, which is one of the possible answers.
In order to solve this problem, we need to find a point that will satisfy both equations. In order to do this, we need to combine the two equations into a single expression. For this, we need to isolate either x or y in one of the equations. Since the equation
Now that we have two possible values for x, we can plug each value into either equation to obtain two values for y. For
Compare your answer with the correct one above
Find the distance between the points 
and 
.
Find the distance between the points
The easiest way to find the distance between two points whose coordinates are given in the form 
and 
is to use the distance formula.
Plugging in the coordinates from our given points, our formula looks as follows
We then simply simplify step by step
Therefore, the distance between the two points is 13.
The easiest way to find the distance between two points whose coordinates are given in the form
Plugging in the coordinates from our given points, our formula looks as follows
We then simply simplify step by step
Therefore, the distance between the two points is 13.
Compare your answer with the correct one above
What is the midpoint between the points 
and 
?
What is the midpoint between the points
To find the midpoint, find the midpoint (or just average) for the x and y value separately. For the x-value, this means: 
. For the y-value, this means: 
. Thus, the midpoint is (3,4).
To find the midpoint, find the midpoint (or just average) for the x and y value separately. For the x-value, this means:
Compare your answer with the correct one above
Find the distance between the two points 
and 
.
Find the distance between the two points
Instead of memorizing the distance formula, think of it as a way to use the Pythagorean Theorem. In this case, if you draw both points on a coordinate system, you can draw a right triangle using the two points as corners. The result is a 5-12-13 triangle. Thus, the missing side's length is 13 units. If you don't remember this triplet, then you could use the Pythagorean Theorem to solve.
Instead of memorizing the distance formula, think of it as a way to use the Pythagorean Theorem. In this case, if you draw both points on a coordinate system, you can draw a right triangle using the two points as corners. The result is a 5-12-13 triangle. Thus, the missing side's length is 13 units. If you don't remember this triplet, then you could use the Pythagorean Theorem to solve.
Compare your answer with the correct one above
What is the measurement of 
?
What is the measurement of
Whenever you have an angle that is inscribed to the outside edge of a circle and to an angle that passes through the midpoint of the circle, the inscribed angle will always be one half the measurement of the angle that passes through the midpoint of the circle.
Since the angle that passes through the midpoint of the circle is a straight angle (all straight angles measure 
degrees), the inscribed angle must measure 
degrees.
Since the sum of the internal angles of all triangles add up to 
degrees, add up the measurements of the angles that you know and subtract the sum from 
degrees to find your answer:
Whenever you have an angle that is inscribed to the outside edge of a circle and to an angle that passes through the midpoint of the circle, the inscribed angle will always be one half the measurement of the angle that passes through the midpoint of the circle.
Since the angle that passes through the midpoint of the circle is a straight angle (all straight angles measure
Since the sum of the internal angles of all triangles add up to
Compare your answer with the correct one above
What is the measurement of 
?
What is the measurement of
If you extend the lines of the parellelogram, you will notice that a parellogram is the same as 2 different sets of parellel lines intersecting one another. When that happens, the following angles are congruent to one another:
Therefore, 
If you extend the lines of the parellelogram, you will notice that a parellogram is the same as 2 different sets of parellel lines intersecting one another. When that happens, the following angles are congruent to one another:
Therefore,
Compare your answer with the correct one above
In a poll, Camille learned that 
of her classmates spoke English at home, 
spoke Spanish, and 
spoke other languages. If she were to graph this data on a pie chart, what would be the degree measurement for the part representing students who speak Spanish at home?
In a poll, Camille learned that
In order to solve this problem, you must first solve for what percentage of the entire group comprise of Spanish-speaking students. To do this, divide the total amount of Spanish-speaking students by the total number of students.
Multiply this number by 100 and round up in order to get your percentage.
Then, multiply this number times the total degrees in a circle to find out the measurement of the piece representing Spanish-speaking students on the pie chart.
Round up:
In order to solve this problem, you must first solve for what percentage of the entire group comprise of Spanish-speaking students. To do this, divide the total amount of Spanish-speaking students by the total number of students.
Multiply this number by 100 and round up in order to get your percentage.
Then, multiply this number times the total degrees in a circle to find out the measurement of the piece representing Spanish-speaking students on the pie chart.
Round up:
Compare your answer with the correct one above
Which of the following is the slope-intercept form of 
?
Which of the following is the slope-intercept form of
To answer this question, we must put the equation into slope-intercept form, meaning we must solve for 
. Slope-intercept form follows the format 
where 
is the slope and 
is the intercept.
Therefore, we must solve the equation so that 
is by itself. First we add 
to both sides so that we can start to get 
by itself:
Then, we must subtract 
from both sides:
We then must divide each side by 
Therefore, the slope-intercept form of the original equation is 
.
To answer this question, we must put the equation into slope-intercept form, meaning we must solve for
Therefore, we must solve the equation so that
Then, we must subtract
We then must divide each side by
Therefore, the slope-intercept form of the original equation is
Compare your answer with the correct one above
Following the line 
, what is the distance from the the point where 
to the point where 
?
Following the line
The first step is to find the y-coordinates for the two points we are using. To do this we plug our x-values into the equation. Where 
, we get 
, giving us the point 
. Where 
, we get 
, giving us the point 
.
We can now use the distance formula: 
.
Plugging in our points gives us 
The first step is to find the y-coordinates for the two points we are using. To do this we plug our x-values into the equation. Where
We can now use the distance formula:
Plugging in our points gives us
Compare your answer with the correct one above
The coordinates of the endpoints of 
, in the standard 
coordinate plane, are 
and 
. What is the 
-coordinate of the midpoint of ?
The coordinates of the endpoints of
To answer this question, we need to find the midpoint of 
.
To find how far the midpoint of a line is from each end, we use the following equation:
and 
are taken from the 
value of the second point and 
and 
are taken from the 
value of the first point. Therefore, for this data:
We can then solve:
Therefore, our midpoint is 
units between each endpoint's 
value and 
unit between each endpoint's 
value. To find out the location of the midpoint, we subtract the midpoint distance from the 
point. (In this case it's the point 
.) Therefore:
So the midpoint is located at 
The question asked us what the 
-coordinate of this point was. Therefore, our answer is 
.
To answer this question, we need to find the midpoint of
To find how far the midpoint of a line is from each end, we use the following equation:
We can then solve:
Therefore, our midpoint is
So the midpoint is located at
The question asked us what the
Compare your answer with the correct one above
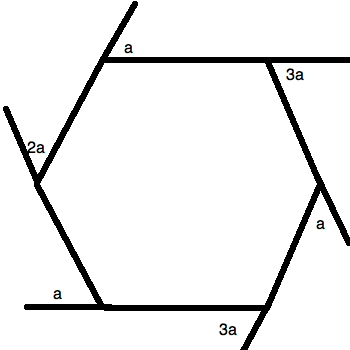
All of the angles marked are exterior angles.
What is the value of 
in degrees? Round to the nearest hundredth.
All of the angles marked are exterior angles.
What is the value of
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
, where 
is the number of sides.
Therefore, a hexagon like this one has:
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
. Since there are 
angles, you know that the numeric portion will be 
or 
. Thus, you can write:
Simplify and solve for 
:
This is 
or 
.
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
Therefore, a hexagon like this one has:
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to
Simplify and solve for
This is
Compare your answer with the correct one above
The sum of all the angles inside of a regular hexagon is 
. Determine the value of one angle.
The sum of all the angles inside of a regular hexagon is
In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to 
. To find the value of one angle, we must divide 
by 
, since there are 
angles inside of a hexagon.
In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to
Compare your answer with the correct one above
The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of 
?
The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
, where 
is the number of sides.
Therefore, a hexagon like this one has:
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
. Thus, you can write:
Solve for 
:
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
Therefore, a hexagon like this one has:
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:
Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to
Solve for
Compare your answer with the correct one above
If the diagonals of the quadrilateral above were drawn in the figure, they would form four 90 degree angles at the center. In degrees, what is the value of 
?
If the diagonals of the quadrilateral above were drawn in the figure, they would form four 90 degree angles at the center. In degrees, what is the value of
A quadrilateral is considered a kite when one of the following is true:
(1) it has two disjoint pairs of sides are equal in length or
(2) one diagonal is the perpendicular bisector of the other diagonal. Given the information in the question, we know (2) is definitely true.
To find 
we must first find the values of all of the angles.
The sum of angles within any quadrilateral is 360 degrees.
Therefore 
.
To find 
:
A quadrilateral is considered a kite when one of the following is true:
(1) it has two disjoint pairs of sides are equal in length or
(2) one diagonal is the perpendicular bisector of the other diagonal. Given the information in the question, we know (2) is definitely true.
To find
The sum of angles within any quadrilateral is 360 degrees.
Therefore
To find
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where 
is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: 
degrees 
degrees 
degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between 
degrees and the non-congruent opposite angles sum by 
:
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above
Using the kite shown above, find the sum of the two remaining congruent interior angles.
Using the kite shown above, find the sum of the two remaining congruent interior angles.
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
To find the sum of the remaining two angles, determine the difference between degrees and the sum of the non-congruent opposite angles.
The solution is:
degrees
Thus, 
degrees is the sum of the remaining two opposite angles.
Check:
The sum of the interior angles of any polygon can be found by applying the formula:
By definition, a kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
To find the sum of the remaining two angles, determine the difference between
The solution is:
Thus,
Check:
Compare your answer with the correct one above
A kite has one set of opposite interior angles where the two angles measure 
and 
, respectively. Find the measurement for one of the two remaining interior angles in this kite.
A kite has one set of opposite interior angles where the two angles measure
The sum of the interior angles of any polygon can be found by applying the formula:
degrees, where is the number of sides in the polygon.
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal: degrees degrees degrees. Additionally, kites must have two sets of equivalent adjacent sides & one set of congruent opposite angles.
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between degrees and the non-congruent opposite angles sum by :
This means that 
is the sum of the remaining two angles, which must be opposite congruent angles. Therefore, the measurement for one of the angles is:
The sum of the interior angles of any polygon can be found by applying the formula:
A kite is a polygon with four total sides (quadrilateral). The sum of the interior angles of any quadrilateral must equal:
The missing angle can be found by finding the sum of the non-congruent opposite angles. Then divide the difference between
This means that
Compare your answer with the correct one above