Sectors - ACT Math
Card 0 of 20

The sector pictured above is  of the circle. What is the angle measure
of the circle. What is the angle measure  for the sector?
for the sector?

The sector pictured above is 

A question like this is very easy. You merely need to find out what is  of the total
of the total  degrees in a circle. This is:
degrees in a circle. This is:
 . That is it!
. That is it!
A question like this is very easy. You merely need to find out what is 


Compare your answer with the correct one above

The area of sector  is
is  . This figure is not drawn to scale.
. This figure is not drawn to scale.
What is the measure of the angle of the sector?

The area of sector 

What is the measure of the angle of the sector?
You know that the area of a circle is computed by the equation:

For our data, this is:
 or
or 
Now, the sector is a percentage of the circle. For the areas, this can be represented as the fraction:

The total degree measure of a circle is, of course,  degrees. This means that the sector contains:
degrees. This means that the sector contains:
 .
.
You know that the area of a circle is computed by the equation:
For our data, this is:

Now, the sector is a percentage of the circle. For the areas, this can be represented as the fraction:
The total degree measure of a circle is, of course, 

Compare your answer with the correct one above

The arc length of sector above is  . This figure is not drawn to scale.
. This figure is not drawn to scale.
What is the angle measure of sector  ?
?

The arc length of sector above is 
What is the angle measure of sector 
You know that the circumference of a circle is computed by the equation:

For our data, this is:

Now, the sector is a percentage of the circle. For the lengths of the circumference and the arc length, this can be represented as the fraction:

The total degree measure of a circle is, of course,  degrees. This means that the sector contains:
degrees. This means that the sector contains:
 .
.
You know that the circumference of a circle is computed by the equation:
For our data, this is:
Now, the sector is a percentage of the circle. For the lengths of the circumference and the arc length, this can be represented as the fraction:
The total degree measure of a circle is, of course, 

Compare your answer with the correct one above

Sector  is
is  of the total circle. This figure is not drawn to scale.
of the total circle. This figure is not drawn to scale.
What is the angle of this sector?

Sector 

What is the angle of this sector?
Do not overthink this question! All you need to remember is that a given circle contains  degrees. This means that the sector is merely a percentage of
degrees. This means that the sector is merely a percentage of  . For our question, this percentage is
. For our question, this percentage is  , which is the same as
, which is the same as  . So, to calculate, you merely need to multiply:
. So, to calculate, you merely need to multiply:

This is the degree measure of the sector.
Do not overthink this question! All you need to remember is that a given circle contains 



This is the degree measure of the sector.
Compare your answer with the correct one above
A bike wheel has  evenly spaced spokes spreading from its center to its tire. What must the angle be for the spokes in order to guarantee this even spacing? Round to the nearest hundredth.
evenly spaced spokes spreading from its center to its tire. What must the angle be for the spokes in order to guarantee this even spacing? Round to the nearest hundredth.
A bike wheel has 
Remember that the total degree measure of a circle is  . This means that if you have
. This means that if you have  parts into which you have divided your circle, each spoke must be
parts into which you have divided your circle, each spoke must be  or
or  apart.
apart.
Remember that the total degree measure of a circle is 



Compare your answer with the correct one above

In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Compare your answer with the correct one above
What is the angle of a sector of area 
 on a circle having a radius of
on a circle having a radius of  ?
?
What is the angle of a sector of area 


To begin, you should compute the complete area of the circle:

For your data, this is:

Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:

Now, multiply this by the total  degrees in a circle:
degrees in a circle:

Rounded, this is  .
.
To begin, you should compute the complete area of the circle:
For your data, this is:
Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:
Now, multiply this by the total 
Rounded, this is 
Compare your answer with the correct one above
What is the angle of a sector that has an arc length of 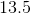
 on a circle of diameter
on a circle of diameter 
 ?
?
What is the angle of a sector that has an arc length of 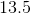



The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:

For your data, this means,

Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:

Rounded to the nearest hundredth, this is  .
.
The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 
Compare your answer with the correct one above

The radius of the circle above is  and
and  . What is the area of the shaded section of the circle?
. What is the area of the shaded section of the circle?

The radius of the circle above is 

Area of Circle = πr2 = π42 = 16π
Total degrees in a circle = 360
Therefore 45 degree slice = 45/360 fraction of circle = 1/8
Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π
Area of Circle = πr2 = π42 = 16π
Total degrees in a circle = 360
Therefore 45 degree slice = 45/360 fraction of circle = 1/8
Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π
Compare your answer with the correct one above
Stan is making some giant circular pies for his friend's wedding. The pies each have a diameter of  and will be cut into
and will be cut into  equal pieces. Stan wants to have three pieces to himself. What is the surface area of the pie that Stan will eat if he eats three pieces?
equal pieces. Stan wants to have three pieces to himself. What is the surface area of the pie that Stan will eat if he eats three pieces?
Stan is making some giant circular pies for his friend's wedding. The pies each have a diameter of 

To begin with, we need to break down the word problem to figure out exactly what is being asked of us. We are given a diameter and some clues about how much pie Stan wants to eat.
To solve this problem, we will go through a few steps. First, we have to find the area of a whole pie. Then, we have to find the area of one slice of pie. Finally, we have to multiply the area of a slice of pie by  , since Stan wants to eat three slices of pie, not just one.
, since Stan wants to eat three slices of pie, not just one.
To find the area of a whole pie, we will need to recall the formula for area of a circle:

In this case, we aren't given  , but we do know
, but we do know  , which is equal to
, which is equal to  . Since
. Since  ,
,  . Substituting
. Substituting  for
for  into the equation for an area of a circle, we get:
into the equation for an area of a circle, we get:

Each of the answer choices includes  , so don't change
, so don't change  into a decimal.
into a decimal.
Next, to find the area of one slice of pie, we want to multiply the total area of the circle by the fractional area we are interested in.
We are told in the question that one slice is equivalent to  of the pie since each pie will be cut into
of the pie since each pie will be cut into  slices. We also know that Stan wants to eat three slices of pie. Therefore, we will need to multiply the total area by
slices. We also know that Stan wants to eat three slices of pie. Therefore, we will need to multiply the total area by  .
.
So, to find the total area of pie that Stan wants to eat, we will perform the following calculation:

So, Stan wants to eat  of pie.
of pie.
To begin with, we need to break down the word problem to figure out exactly what is being asked of us. We are given a diameter and some clues about how much pie Stan wants to eat.
To solve this problem, we will go through a few steps. First, we have to find the area of a whole pie. Then, we have to find the area of one slice of pie. Finally, we have to multiply the area of a slice of pie by 
To find the area of a whole pie, we will need to recall the formula for area of a circle:
In this case, we aren't given 






Each of the answer choices includes 

Next, to find the area of one slice of pie, we want to multiply the total area of the circle by the fractional area we are interested in.
We are told in the question that one slice is equivalent to 


So, to find the total area of pie that Stan wants to eat, we will perform the following calculation:
So, Stan wants to eat 
Compare your answer with the correct one above
If a circle,  , is centered at the origin, and has an area of
, is centered at the origin, and has an area of  , what is the area of the sector defined by the lines
, what is the area of the sector defined by the lines  and the
and the  -axis?
-axis?
If a circle, 



Our first step is to find the angle between the lines  and the x-axis. Because one of our lines is the x-axis, we can do this by simply taking the inverse-tangent of the slope of
and the x-axis. Because one of our lines is the x-axis, we can do this by simply taking the inverse-tangent of the slope of  . We know the slope of
. We know the slope of  is equal to 1.
is equal to 1.
 radians or
radians or  degrees. There are
degrees. There are  radians or
radians or  degrees in a circle. Dividing our angle by the whole, we see that our angle is
degrees in a circle. Dividing our angle by the whole, we see that our angle is  of a complete circle.
of a complete circle.
Therefore, the area of our sector must be  of the total area of the circle.
of the total area of the circle.  .
.
Our first step is to find the angle between the lines 







Therefore, the area of our sector must be 

Compare your answer with the correct one above
A pizza recipe requires  drops of hot sauce for every
drops of hot sauce for every  of surface area. If these drops are evenly distributed, what is the amount of hot sauce on a piece of pizza that is
of surface area. If these drops are evenly distributed, what is the amount of hot sauce on a piece of pizza that is  in diameter, cut into
in diameter, cut into  pieces? Round to the nearest drop. Assume that the sauce is evenly spread.
pieces? Round to the nearest drop. Assume that the sauce is evenly spread.
A pizza recipe requires 



To start, calculate the total area of the pizza. This is easily done, using the equation for the area of a circle:

Be careful, though. Notice that they give you the diameter, so the radius is  :
:

Now, if this is cut into eight pieces, this would be:
 or approximately
or approximately 
 per piece.
per piece.
Now, you need to divide this by  to find out the drop amount:
to find out the drop amount:

For your answer, you will round to  .
.
To start, calculate the total area of the pizza. This is easily done, using the equation for the area of a circle:
Be careful, though. Notice that they give you the diameter, so the radius is 
Now, if this is cut into eight pieces, this would be:



Now, you need to divide this by 
For your answer, you will round to 
Compare your answer with the correct one above
A group of students wish to cut a circular pizza of diameter  into equal slices, each with an angle of
into equal slices, each with an angle of  . What is the total surface area, in square inches, of each slice of pizza? Round to the nearest hundredth.
. What is the total surface area, in square inches, of each slice of pizza? Round to the nearest hundredth.
A group of students wish to cut a circular pizza of diameter 

A group of students wish to cut a circular pizza of diameter 
 into pieces with an angle of
into pieces with an angle of  degrees. What is the total surface area of pizza that each student will recieve if every student eats two pieces of pizza?
degrees. What is the total surface area of pizza that each student will recieve if every student eats two pieces of pizza?
To solve a question like this, you need to compute the percentage of the circle that will be represented by a cut of  degrees. The total equation for this is:
degrees. The total equation for this is:

The total area is found merely by using the standard equation for the area of a circle:

For your data, this is:

Multiply this by  and you get approximately
and you get approximately 

A group of students wish to cut a circular pizza of diameter 


To solve a question like this, you need to compute the percentage of the circle that will be represented by a cut of 
The total area is found merely by using the standard equation for the area of a circle:
For your data, this is:
Multiply this by 

Compare your answer with the correct one above
On a circle with a radius of  , what is the area of a sector having an arc length of
, what is the area of a sector having an arc length of  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
On a circle with a radius of 

To solve this, you need to find the percentage of the given arc with respect to the total circumference. The total circumference of your circle is found merely by using:
 or, for your data
or, for your data 
So, your arc is the following percentage of the circle:
 or approximately
or approximately 
Now, the total area of your circle is:
 or
or 
Your sector will be merely  times
times  or
or  .
.
To solve this, you need to find the percentage of the given arc with respect to the total circumference. The total circumference of your circle is found merely by using:

So, your arc is the following percentage of the circle:

Now, the total area of your circle is:

Your sector will be merely 


Compare your answer with the correct one above
Find the area of a 90 degree sector of a circle whose radius is 2.
Find the area of a 90 degree sector of a circle whose radius is 2.
To solve, first find area. Substitute 2 in for the radius.

Then, to find the area of a sector, divide 90 by the total degrees in a circle and multiply it by the area.
Thus,

To solve, first find area. Substitute 2 in for the radius.
Then, to find the area of a sector, divide 90 by the total degrees in a circle and multiply it by the area.
Thus,
Compare your answer with the correct one above

In the circle above, the angle A in radians is 
What is the length of arc A?

In the circle above, the angle A in radians is
What is the length of arc A?
Circumference of a Circle = 
Arc Length




Circumference of a Circle =
Arc Length
Compare your answer with the correct one above
If a circle has a circumference of  , what is the measure of the arc contained by a
, what is the measure of the arc contained by a  degree angle located at the center of the circle?
degree angle located at the center of the circle?
If a circle has a circumference of 

A circle has a total of  degrees. If our angle is located at the center and is
degrees. If our angle is located at the center and is  degrees, we can do
degrees, we can do  to see that our angle makes up
to see that our angle makes up  of the complete circle.
of the complete circle.
Therefore, our arc is going to be  of our total circumference.
of our total circumference. 
A circle has a total of 



Therefore, our arc is going to be 
Compare your answer with the correct one above

The figure above is a circle with center at  and a radius of
and a radius of  . This figure is not drawn to scale.
. This figure is not drawn to scale.
What is the length of the arc  in the figure above?
in the figure above?

The figure above is a circle with center at 

What is the length of the arc 
Recall that the length of an arc is merely a percentage of the circumference. The circumference is found by the equation:

For our data, this is:

Now the percentage for our arc is based on the angle  and the total degrees in a circle, namely,
and the total degrees in a circle, namely,  .
.
So, the length of the arc is:

Recall that the length of an arc is merely a percentage of the circumference. The circumference is found by the equation:
For our data, this is:
Now the percentage for our arc is based on the angle 

So, the length of the arc is:
Compare your answer with the correct one above
What is the length of the arc  ?
?

The total area of the circle is  and the area of the shaded region is
and the area of the shaded region is  .
.
What is the length of the arc 

The total area of the circle is 

If the area of the circle is  , the radius can be found using the formula for the area of a circle:
, the radius can be found using the formula for the area of a circle:

For our data, this is:


Therefore, 
Now, the circumference of the circle is defined as:

For our data, this is:

Now, we know that a sector is a percentage of the total area. This percentage is easily calculated:

So, the length of the arc will merely be the same percentage, but now applied to the circumference:

If the area of the circle is 
For our data, this is:
Therefore,
Now, the circumference of the circle is defined as:
For our data, this is:
Now, we know that a sector is a percentage of the total area. This percentage is easily calculated:
So, the length of the arc will merely be the same percentage, but now applied to the circumference:
Compare your answer with the correct one above
What is the area of the sector of a circle with a central angle of  degrees and a radius of
degrees and a radius of  ? Simplify any fractions and leave your answer in terms of
? Simplify any fractions and leave your answer in terms of  .
.
What is the area of the sector of a circle with a central angle of 


The formula for the area of a sector of a circle is:

The central angle given is 120 thus:

The formula for the area of a sector of a circle is:
The central angle given is 120 thus:
Compare your answer with the correct one above