Groups - Abstract Algebra
Card 0 of 4
Which of the following is an identity element of the binary operation 
?
Which of the following is an identity element of the binary operation
Defining the binary operation 
will help in understanding the identity element. Say 
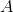is a set and the binary operator is defined as 
for all given pairs in 
.
Then there exists an identity element 
in 
such that given,
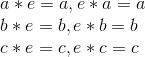
Therefore, looking at the possible answer selections the correct answer is,
Defining the binary operation
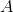
Then there exists an identity element
Therefore, looking at the possible answer selections the correct answer is,
Compare your answer with the correct one above
Which of the following illustrates the inverse element?
Which of the following illustrates the inverse element?
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every 
such that 
where 
and 
is an identity element.
For every element in a set, there exists another element that when they are multiplied together results in the identity element.
In mathematical terms this is stated as follows.
For every
Compare your answer with the correct one above
identify the following definition.
Given 
is a normal subgroup of 
, it is denoted that 
when the group of left cosets of 
in 
is called __________.
identify the following definition.
Given
By definition of a factor group it is stated,
Given 
is a normal subgroup of 
, it is denoted that 
when the group of left cosets of 
in 
is called the factor group of 
which is determined by 
.
By definition of a factor group it is stated,
Given
Compare your answer with the correct one above
Determine whether the statement is true of false:
Determine whether the statement is true of false:
This statement is true based on the following theorem.
For all 
, 
in 
.
If 
is a normal subgroup of 
then the cosets of 
forms a group under the multiplication given by,
This statement is true based on the following theorem.
For all
If
Compare your answer with the correct one above